Este é um estudo de caso baseado no estudo realizado no capítulo 2 do livro Digital Control in Power Electronics escrito por Simone Buso (University of Padovia, Itália) e Paolo Mattavelli (Univerisity of Udina, Itália).
Há algum tempo, o esgotamento das energias convencionais, que provém de combustíveis fósseis, e também a constante e crescente demanda de energia vem voltando atenção para que a sociedade se torne cada vez mais sustentável e busque cada vez mais a utilização de energias consideradas renováveis.
A geração de energia centralizada, que é o modelo tradicional e que, muitas vezes emprega combustíveis fosseis é um modelo de geração insustentável em logo prazo e, por isso, as fontes de energias renováveis, que são reabastecidas de maneira continua pela natureza, vem ganhando bastante destaque e muita notoriedade na área da pesquisa e também no mercado.
Por essas e outras razões, o modelo de geração distribuída, que se opõe ao modelo tradicional, uma vez que ele é caracterizado pelo uso de geradores descentralizados, ou seja, eles vão ser instalados mais próximo do dos locais de consumo e, no modelo tradicional, os geradores são construídos mais distantes dos consumidores, tem ganhado cada vez mais destaque no Brasil e no mundo.
Fontes renováveis, como a fotovoltaica e a eólica, utilizam recursos da natureza para gerar energia em corrente contínua e, para que essa energia seja utilizada pelo consumidor ou até injetada na rede, de uma forma adequada, é necessário que haja o seu condicionamento. O condicionamento nada mais é que a conversão do sinal de tensão CC obtido da fonte renovável, para uma forma de onda de tensão com características de fase, de amplitude, de distorção harmônica e de frequência que vão satisfazer a operação da rede elétrica.
Por esse e outros motivos, o tópico deste texto está relacionado com a eletrônica de potência, que irá desempenhar um papel fundamental no condicionamento da forma de onda. Através dela, controlando os conversores eletrônicos de potência, é possível alcançar algumas funcionalidades do sistema de geração distribuída.
Um inversor é um circuito que irá converter CC em CA, transferindo potência de uma fonte CC para uma carga CA. Neste estudo de caso, avaliaremos um inversor na topologia de ponte H completa para o qual determinaremos o diagrama de blocos do controle do inversor e definiremos os ganhos Kp e Ki para o controlador.
Como definir o ganho do PWM?
É possível fazer uma interpretação geométrica da relação entre a modulação (m), a portadora triangular e o duty cycle, tornando possível determinar o ganho do PWM. Neste processo, algumas considerações precisam ser feitas. Entre elas, o período da modulante (m) tem de ser muito maior que o período da portadora, uma vez que há a necessidade de considerar uma variação infinitesimal em um determinado espaço de tempo, possibilitando a aproximação da curva m(t) para uma reta.
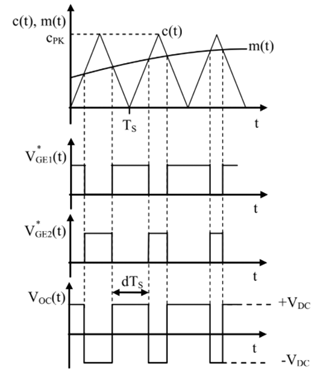
Fonte: Buso & Mattavelli (2015)
Na figura 1, é possível observar a forma de onda da portadora triangular e da modulação (m) com um período Ts de tempo.
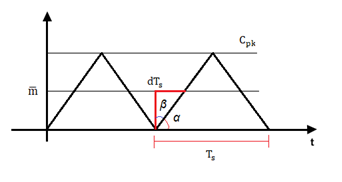
Fonte: Autora (2022)
Em busca da obtenção de uma relação geométrica entre as duas formas de onda, considera-se Cpk como sendo a amplitude da portadora e que ϴ e α são ângulos complementares. Sendo assim;
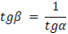
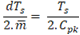
Consequentemente, é possível determinar a relação do duty cycle com a modulante e, em seguida, perceber que o ganho do PWM será de 1/Cpk.
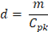
Como definir o delay associado ao PWM?
Pela natureza do PWM ser digital, existe um delay que deve ser considerado. Ao considerar um atraso de Ts/2, obtém-se a seguinte função de transferência para o delay:
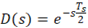
Utilizando a aproximação de Padé, é possível obter:
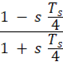
Como chegar na função de transferência do controlador PI?
O controlador Proporcional Integral irá gerar um resultado, u(t) da combinação das saídas proporcional e integral. Dessa forma, tem-se:
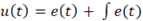
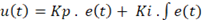
Deve-se então definir a função de transferência do controlador PI. Para isso, é aplicada a transformada de Laplace, obtendo:
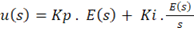
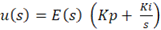
Sendo, E(s) e u(s), respectivamente, a entrada e a saída do sistema, pode-se determinar a função de transferência como (Ogata, 2003):
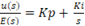
Como encontrar o ganho do inversor com ponte H completa?
Para obter o ganho nesta etapa, utilizaremos um inversor em ponte H completa, que está sendo representada, com suas respectivas variáveis, na figura 4. É válido lembrar que esta figura é apenas um modo de representação simplificado e esboçado no software PSIM e que, nela não estão representadas os labels, que são as saídas do PWM, cujo código deverá ser implementado através do bloco C, e que irão controlar a comutação dos IGBTs. A implementação do PWM no bloco C do PSIM será tópico futuro de outro texto neste blog.
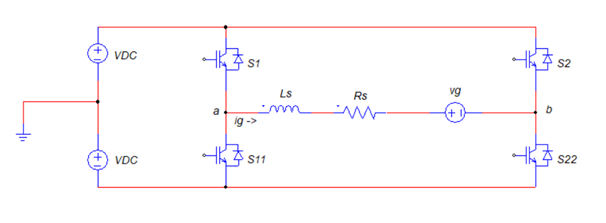
Fonte: Autora (2022)
Por conta da amplitude da modulação PWM, define-se que:
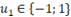
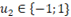
Analisando o circuito, pode-se obter:
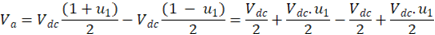
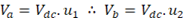
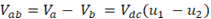
Sendo assim, é considerar três estados possíveis para a tensão Vab:
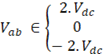
Como a modulação, neste caso, é unipolar, definimos :
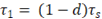
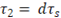
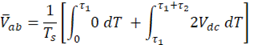
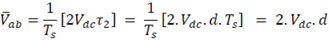
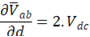
Portanto, o ganho do inversor é dado por 2VDC.
Como definir a função de transferência da carga associada ao sistema?
Ainda utilizando o modelo da Figura 4, para definir a função de transferência da carga do sistema, considera-se que Vg é constante, uma vez que se deve observar apenas a dinâmica entre Vab e a corrente ig. Então:
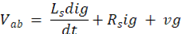
Sendo assim:
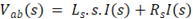
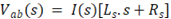
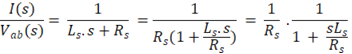
Pode-se então, definir a função de transferência da carga como sendo
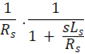
Abaixo é possível observar o diagrama de blocos da malha de controle completa para o sistema em questão. Existe ainda, a necessidade de determinar os parâmetros Kp e Ki para o controlador do sistema, cuja dedução será detalhada em um texto futuro, mas que, para o sistema em questão, podem ser encontrados através do código do exemplo. A funções de Kp e Ki implementadas neste código do matlab são oriundas do próprio livro texto Digital Control in Power Electronics.
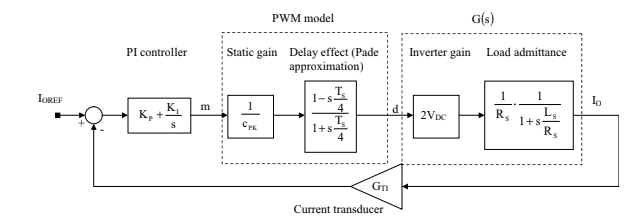
Fonte: Buso & Mattavelli (2015)
Exemplo
Como exemplo, Buso & Mattavelli sugerem em seu livro, um sistema com parâmetros (tensão do link DC, frequência de chaveamento, resistência e indutância da carga, entre outros) definidos. A partir deles, é possível encontrar os parâmetros Kp e Ki do controlador e definir a constante de tempo do controlador PI, executando o código abaixo no matlab.
clear all
close all
clc
%DADOS
Rs = 1; %phase resistence
Ls = 1.5e-3; %Phase inductance
%fs = 125; % load frequency
Es = 100; %phase load voltage
w0 = 2*pi*125;
Vdc = 250; % DC link voltage
fsw = 50e3; %switching frequency / frequencia do PWM
wsw = 2*pi*fsw; %freq pwm em rad
Ts = 1/fsw; %periodo do chaveamento
Gti = 0.1; %current transducer gain
cpk = 4; % pwm carrier peak
%parametros de projeto
wCL = wsw/6; % freq de cruzamento
phm = 60*pi/180; % margem de fase
Kp = cpk*Rs*sqrt(1 + (wCL*Ls/Rs)^2)/(2*Vdc*Gti)
dKi = tan(-pi/2 + phm + 2*atan(wCL*Ts/4) + atan(wCL*Ls/Rs));
Ki = wCL*Kp/dKi
Ti = Kp/Ki %constante de tempo do PI
Referências
BUSO, Simone; MATTAVELLI, Paolo. Digital control in power electronics. Synthesis Lectures on Power Electronics, v. 5, n. 1, p. 1-229, 2015.
OGATA, Katsuhiko. Engenharia de controle moderno, Ed. Sao Paulo: 4o, 2003.
HART, Daniel W. Eletrônica de potência: análise e projetos de circuitos. McGraw Hill Brasil, 2016.




Sobre o Autor